Introduction to Machine Learning – IITKGP Week 4 NPTEL Assignment Answers 2025

Need help with this week’s assignment? Get detailed and trusted solutions for Introduction to Machine Learning – IITKGP Week 4 NPTEL Assignment Answers. Our expert-curated answers help you solve your assignments faster while deepening your conceptual clarity.

✅ Subject: Introduction to Machine Learning – IITKGP (nptel ml Answers)
📅 Week: 4
🎯 Session: NPTEL 2025 July-October
🔗 Course Link: Click Here
🔍 Reliability: Verified and expert-reviewed answers
📌 Trusted By: 5000+ Students

For complete and in-depth solutions to all weekly assignments, check out 👉 NPTEL Introduction to Machine Learning – IITKGP Week 4 Assignment Answers

🚀 Stay ahead in your NPTEL journey with fresh, updated solutions every week!

NPTEL Introduction to Machine Learning – IITKGP Week 4 Assignment Answers 2025

1. A man is known to speak the truth 2 out of 3 times. He throws a die and reports that the number
obtained is 4. Find the probability that the number obtained is actually 4 :

A. 2/3
B. 3/4
C. 5/22
D. 2/7

Answer : See Answers

2.

Answer :

3. Two cards are drawn at random from a deck of 52 cards without replacement. What is the probability of drawing a 2 and an Ace in that order?

A. 4/51
B. 1/13
C. 4/256
D. 4/663

Answer :

4.

Answer :

5. What is the naive assumption in a Naive Bayes Classifier?

A. All the classes are independent of each other
B. All the features of a class are independent of each other
C. The most probable feature for a class is the most important feature to be considered for classification
D. All the features of a class are conditionally dependent on each other.

Answer :

6. A drug test (random variable T) has 1% false positives (i.e., 1% of those not taking drugs show positive in the test), and 5% false negatives (i.e., 5% of those taking drugs test negative). Suppose that 2% of those tested are taking drugs. Determine the probability that somebody who tests positive is actually taking drugs (random variable D).

A. 0.66
B. 0.34
C. 0.50
D. 0.91

Answer : See Answers

7.

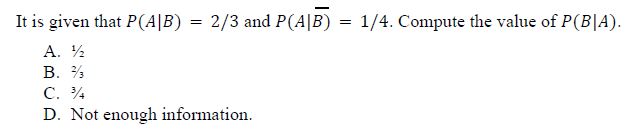
Answer :

8. What is the joint probability distribution in terms of conditional probabilities?

A. P(D1) * P(D2|D1) * P(S1|D1) * P(S2|D1) * P(S3|D2)
B. P(D1) * P(D2) * P(S1|D1) * P(S2|D1) * P(S3|D1, D2)
C. P(D1) * P(D2) * P(S1|D2) * P(S2|D2) * P(S3|D2)
D. P(D1) * P(D2) * P(S1(D1) * P(S2|D1, D2) * P(S3|D2)

Answer :

9. Suppose P(D1) = 0.5. P(D2)=0.6 . P(S1|D1)=0.4 and P(S1| D1′)= 0.6. Find P(S1)

A. 0.14
B. 0.36
C. 0.50
D. 0.66

Answer :

10. In a Bayesian network a node with only outgoing edge(s) represents

A. a variable conditionally independent of the other variables.
B. a variable dependent on its siblings.
c. a variable whose dependency is uncertain.
D. None of the above.

Answer : See Answers