Reinforcement Learning Week 1 NPTEL Assignment Answers 2025

Need help with this week’s assignment? Get detailed and trusted solutions for Reinforcement Learning Week 1 NPTEL Assignment Answers. Our expert-curated answers help you solve your assignments faster while deepening your conceptual clarity.

✅ Subject: Reinforcement Learning
📅 Week: 1
🎯 Session: NPTEL 2025 July-October
🔗 Course Link: Click Here
🔍 Reliability: Verified and expert-reviewed answers
📌 Trusted By: 5000+ Students

For complete and in-depth solutions to all weekly assignments, check out 👉 NPTEL Reinforcement Learning Week 1 NPTEL Assignment Answers

🚀 Stay ahead in your NPTEL journey with fresh, updated solutions every week!

NPTEL Reinforcement Learning Week 1 Assignment Answers 2025

1. In the update rule Q_t+1(a)←Q_t(a)+α(R_t−Q_t(a)), select the value of α that we would prefer to estimate Q values in a non-stationary bandit problem.

Answer : For Answers Click Here 

2. The “Credit assignment problem” is the issue of assigning a correct mapping of rewards accumulated by the action(s). Which of the following is/are the reason for credit assignment problem in RL? (Select all that apply)

• Reward for an action may only be observed after many time steps.
• An agent may get the same reward for multiple actions.
• The agent discounts rewards that occurred in previous time steps.
• Rewards can be positive or negative

Answer :

3. Assertion1: In stationary bandit problems, we can achieve asymptotically correct behaviour by selecting exploratory actions with a fixed non-zero probability without decaying exploration.

Assertion2: In non-stationary bandit problems, it is important that we decay the proba- bility of exploration to zero over time in order to achieve asymptotically correct behavior.

• Assertion1 and Assertion2 are both True.
• Assertion1 is True and Assertion2 is False.
• Assertion1 is False and Assertion2 is True.
• Assertion1 and Assertion2 are both False.

Answer :

4. We are trying different algorithms to find the optimal arm for an multi arm bandit. The expected payoff for each algorithm corresponds to some function with respect to time t (time staring from 0). Given that the optimal expected pay off is 1, which among the following functions corresponds to the algorithm with the least Regret? (Hint: Plot the functions)

• tanh(t/5)
• 1−2^−t
• x/20 if x<20 and 1 after that
• Same regret for all the above functions.

Answer :

5. Which of the following is/are correct and valid reasons to consider sampling actions from a softmax distribution instead of using an ε-greedy approach?
i Softmax exploration makes the probability of picking an action proportional to the action- value estimates. By doing so, it avoids wasting time exploring obviously ’bad’ actions.
ii We do not need to worry about decaying exploration slowly like we do in the ε-greedy case. Softmax exploration gives us asymptotic correctness even for a sharp decrease in temperature.
iii It helps us differentiate between actions with action-value estimates (Q values) that are very close to the action with maximum Q value.

Which of the above statements is/are correct?

• i, ii, iii
• only iii
• only i
• i, ii
• i, iii

Answer :  For Answers Click Here 

6. Consider a standard multi-arm bandit problem. The probability of picking an action, using the softmax policy is given by:

• 0
• 0.13
• 0.232
• 0.143

Answer :

7. What are the properties of a solution method that is PAC Optimal?

• (a) It is guaranteed to find the correct solution.
• (b) It minimizes sample complexity to make the PAC guarantee.
• (c) It always reaches optimal behaviour faster than an algorithm that is simply asymptotically correct.
• Both (a) and (b)
• Both (b) and (c)
• Both (a) and (c)

Answer :

8. Consider the following statements
i The agent must receive a reward for every action taken in order to learn an optimal policy.
ii Reinforcement Learning is neither supervised nor unsupervised learning.
iii Two reinforcement learning agents cannot learn by playing against each other.
iv Always selecting the action with maximum reward will automatically maximize the prob- ability of winning a game.

Which of the above statements is/are correct?

• i, ii, iii
• only ii
• ii, iii
• iii, iv

Answer :

9. Assertion: Taking exploratory actions is important for RL agents
Reason: If the rewards obtained for actions are stochastic, an action which gave a high reward once, might give lower reward next time.

• Assertion and Reason are both true and Reason is a correct explanation of Assertion
• Assertion and Reason are both true and Reason is not a correct explanation of Assertion
• Assertion is true and Reason is false
• Both Assertion and Reason are false

Answer :  For Answers Click Here 

10. Following are two ways for defining the probability of selecting an action/arm in softmax policy. Which among the following is a better choice and why?

• (i) is better choice as it requires less complex computation
• (ii) is better choice as it can also deal with negative values of Q_t(a)
• Both are good as both formulas can bound probability in range 0 to 1.
• (i) is better because it can differentiate well between close values of Q_t(a).

Answer :

NPTEL Reinforcement Learning Week 1 Assignment Answers 2024

1. Which of the following is not a useful way to approach a standard multi-armed bandit problem with n arms? Assume bandits are stationary.

a. “How can I ensure the best action is the one which is mostly selected as time tends to infinity?”
b. “How can I ensure the total regret as time tends to infinity is minimal?”
c. “How can I ensure an arm which has an expected reward within a certain threshold of the optimal arm is chosen with a probability above a certain threshold?”
d. “How can I ensure that when given any 2 arms, I can select the arm with a higher expected return with a probability above a certain threshold?”

Answer: d
Explanation: While (d) sounds reasonable, it’s not typically aligned with the standard objectives of multi-armed bandit problems, which focus on cumulative reward, regret minimization, and PAC-style guarantees, not pairwise arm comparison.

---

2. What is the decay rate of the weightage given to past rewards in the computation of the Q function in the stationary and non-stationary updates in the multi-armed bandit problem?

a. hyperbolic, linear
b. linear, hyperbolic
c. hyperbolic, exponential
d. exponential, linear

Answer: c
Explanation: In stationary settings, average-based updates cause hyperbolic decay of past reward influence. In non-stationary settings (using constant step size α), past rewards decay exponentially.

---

3. In the update rule Qt+1(a) ← Qt(a) + α(Rt − Qt(a)), select the value of α that we would prefer to estimate Q-values in a non-stationary bandit problem.

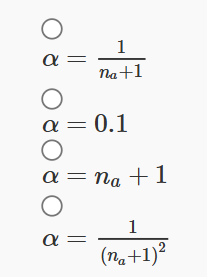
Answer: d
Explanation: In non-stationary problems, a constant α is preferred to give recent rewards more weight and adapt quickly to changes.

---

4. Assertion: Taking exploratory actions is important for RL agents

Reason: If the rewards obtained for actions are stochastic, an action which gave a high reward once, might give lower reward next time.

a. Assertion and Reason are both true and Reason is a correct explanation of Assertion
b. Assertion and Reason are both true and Reason is not a correct explanation of Assertion
c. Assertion is true and Reason is false
d. Both Assertion and Reason are false

Answer: b
Explanation: While both are true, the reason given highlights stochasticity, not the exploration-exploitation tradeoff directly.

---

5. We are trying different algorithms to find the optimal arm for a multi-arm bandit. Which among the following functions will have the least regret?

a. tanh(t)
b. 1 − 2^(−t)
c. x/20 if x < 20 and 1 after that
d. Same regret for all the above functions

Answer: a
Explanation: tanh(t) reaches the optimal value faster than others, which helps reduce cumulative regret in the long run.

---

6. Consider the following statements for ε-greedy in a non-stationary environment:

i. Keeping a small constant ε is a good approach if the environment is non-stationary.
ii. Large ε values lead to unnecessary exploration.
iii. For a stationary environment, decaying ε to zero is a good idea.

a. ii, iii
b. only iii
c. only ii
d. i, ii

Answer: d
Explanation: Statement iii applies to stationary, not non-stationary environments. i and ii are correct in the non-stationary context.

---

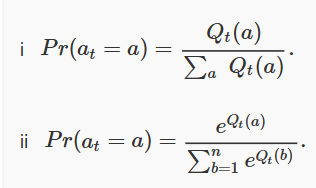
7. Both are good as both formulas can bound probability in range 0 to 1.

(i) is better because it is differentiable and requires less complex computation.
None of the above.

Answer: c
Explanation: Softmax (differentiable) provides a smoother, graded approach to action selection than ε-greedy, especially when Q-values are close.

---

8. Which of the following best refers to PAC-optimality solution to bandit problems?

a. Given δ and ε, minimize the number of steps to reach PAC-optimality (i.e., N)
b. Given δ and N, minimize ε
c. Given ε and N, maximize the probability of choosing optimal arm (i.e., minimize δ)
d. None of the above

Answer: a
Explanation: PAC learning focuses on achieving Probably Approximately Correct solutions within a minimum number of steps.

---

9. Suppose we have a 10-armed bandit problem with deterministic rewards in (0, 10). Which method will allow us to accumulate maximum reward in the long term?

a. ε-greedy with ε = 0.1
b. ε-greedy with ε = 0.01
c. greedy with initial estimates = 0
d. greedy with initial estimates = 10

Answer: d
Explanation: Optimistic initialization encourages early exploration even with greedy methods and allows discovering optimal arms quickly.

---

10. Which of the following are valid reasons to use softmax over ε-greedy?

i. Avoids exploring obviously bad actions
ii. Doesn’t need slow ε decay
iii. Can distinguish close Q-values better

a. i, ii, iii
b. only iii
c. only i
d. i, ii
e. i, iii

Answer: d
Explanation: i and ii are valid; iii is incorrect since softmax doesn’t guarantee better differentiation for close Q-values—it spreads probabilities.