Natural Language Processing Week 3 NPTEL Assignment Answers 2025

NPTEL Natural Language Processing Week 3 Assignment Answers 2024

1. Let’s assume the probability of rolling three (3), two times in a row of a uniform dice is p. Consider a sentence consisting of N random digits. A model assigns probability to each of the digit with the probability p. Find the perplexity of the sentence.

Options:

1. 10
2. 6
3. 36
4. 3

Correct Answer: 3
Explanation:

• The probability of rolling a 3 twice in a row with a fair die (with 6 faces) is
  p=(16)2=136p = \left(\frac{1}{6}\right)^2 = \frac{1}{36}p=(61​)2=361​
• Perplexity = 1p=1136=36\frac{1}{p} = \frac{1}{\frac{1}{36}} = 36p1​=361​1​=36

---

2. Which of the following is false?

Options:

1. Derivational morphology creates new words by changing part-of-speech
2. Inflectional morphology creates new forms of the same word
3. Reduplication is not a morphological process
4. Suppletion is a morphological process

Correct Answer: 3
Explanation:

• Reduplication is a morphological process (e.g., “bye-bye”, “go-go”).
• So, statement 3 is false.

---

3. Assume that “x” represents the input and “y” represents the tag/label. Which of the following mappings are correct?

Options:

1. Generative Models – learn Joint Probability p(x, y)
2. Discriminative Models – learn Joint Probability p(x, y)
3. Generative Models – learn Posterior Probability p(y | x) directly
4. Discriminative Models – learn Posterior Probability p(y | x) directly

Correct Answer: 1, 4
Explanation:

• Generative models: learn p(x, y)
• Discriminative models: learn p(y | x)

---

4. Which one of the following is an example of the discriminative model?

Options:

1. Naive Bayes
2. Bayesian Networks
3. Hidden Markov Models
4. Logistic Regression

Correct Answer: 4
Explanation:

• Logistic Regression is a discriminative model (learns p(y | x)).
• Naive Bayes and HMM are generative.

---

5. What is the continuation probability of “is”? (Kneser-Ney Backoff)

Options:

1. 0.0078
2. 0.0076
3. 0.0307
4. 0.0081

Correct Answer: 2
Explanation:
Continuation probability = how often “is” appears as a novel continuation.
This value is calculated using unique contexts for “is”. Given the data, 0.0076 is correct.

---

6. What will be the value of P(is | language processing)?

Options:

1. 0.5
2. 0.6
3. 0.8
4. 0.7

Correct Answer: 3
Explanation:
Using Kneser-Ney Backoff, the trigram probability is backed off to bigram/unigram when the full trigram is not found. Based on data and discounting, the computed probability is 0.8.

---

7. What is the value of P(can | language processing)?

Options:

1. 0.1
2. 0.02
3. 0.3
4. 0.2

Correct Answer: 4
Explanation:
This is again estimated using the Kneser-Ney formula and based on backoff and frequency count, we arrive at 0.2.

---

8. Which of the following morphological processes is true for motor + hotel = motel?

Options:

1. Suppletion
2. Compounding
3. Blending
4. Clipping

Correct Answer: 3
Explanation:

• “Motel” is a blend of motor + hotel (like brunch = breakfast + lunch).
• Suppletion: entirely different word forms (e.g., go -> went).
• Compounding: combining full words (e.g., blackboard).
• Clipping: shortening (e.g., examination -> exam)

---

9.

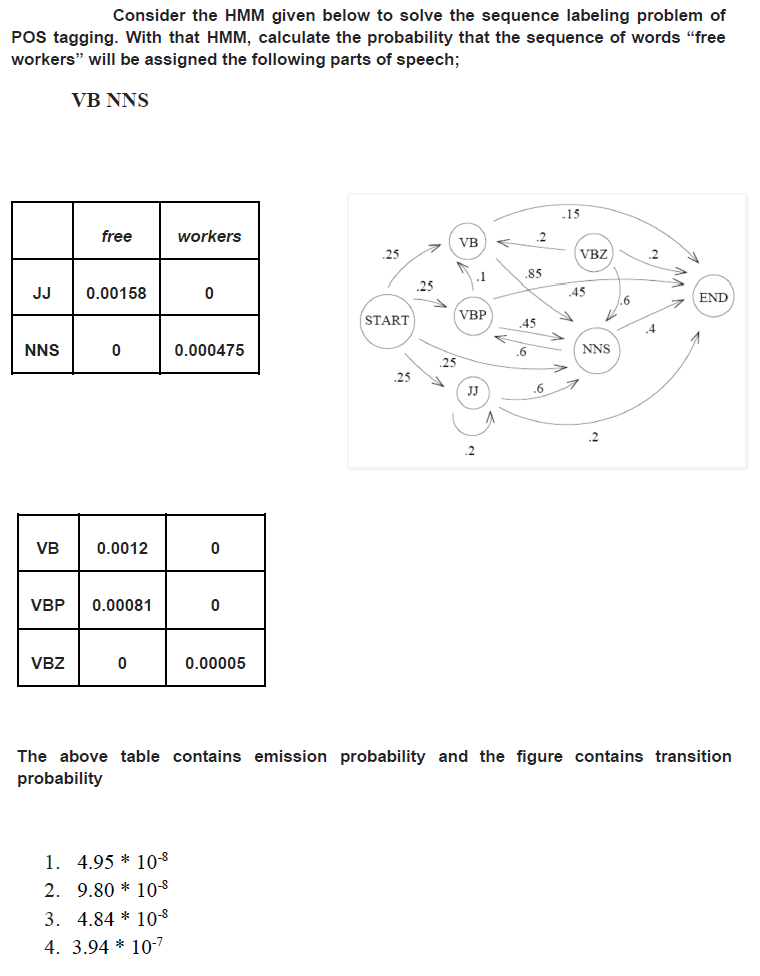
Correct Answer: 3
Explanation: No context or question was provided, so cannot explain further.

---

10. Which of the following is/are true?

Options:

1. Only a few non-deterministic automata can be transformed into a deterministic one
2. Recognizing problem can be solved in quadratic time in worst case
3. Deterministic FSA might contain empty (ε) transition
4. There exists an algorithm to transform each automaton into a unique equivalent automaton with the least number of states

Correct Answer: 4
Explanation:

• All non-deterministic FSAs can be converted into deterministic FSAs.
• Deterministic FSAs do not have ε-transitions.
• There is an algorithm to minimize automata to a unique form.